フォン・ノイマンについて（10）数値予報への貢献2

（このブログは 「気象学と気象予報の発達史 」の一部です。） 

　「（8）電子コンピュータの開発」で述べたフォン・ノイマンが高等研究所で開発していたコンピュータ（IASマシン）が1951年に完成した。この新型の計算機は、ENIACで24時間かかった計算をわずか5分で終える能力を持っていた[1]。この高速の計算機を利用して、1952年にはチャーニーらは、傾圧モデルを用いて低気圧発達の再現に成功した。

　これを受けて、本の「10-5-2 現業運用での数値予報の開始」で述べているように、現業運用のための数値予報モデルの開発のために、1954年にアメリカでは空軍気象局、海軍気象局、アメリカ気象局の三者が「合同数値予報グループ（Joint Numerical Weather Prediction Unit: JNWPU）」を設立した。これは後に、現在アメリカで数値予報を行っている国立環境予報センター（National Center for Environmental Prediction: NCEP）となっていった。

IAS マシンとフォン・ノイマン（右）。左はオッペンハイマー

　1956年にはシカゴ大学の気象学者ノーマン・フィリップス（Norman Phillips, 1923- 2019）が、大気大循環モデルの計算実験を行った。大気大循環モデルとは、気象予測のようなある一定時間後の波の運動の予測ではなく、長期積分によって平均的な大気循環を調べるものである。本の「10-7-2大循環モデルの発明」で述べているように、彼は準地衡風モデルを約30日間走らせることによって、地球上の大気の典型的な気候学的循環パターンの再現に成功した（「気候学の歴史(7)：気候モデルの登場」参照）。

　この大気大循環モデルの成功によって、地球の気候を力学的、熱力学的に調べることができる可能性が出てきた。その将来性に気付いたフォン・ノイマンは、早速大循環モデルのその後の発展のために「Application of Numerical Integration Techniques to the Problem of the General Circulation」と題する会議のお膳立てをした。しかし、がんが進行していたフォン・ノイマンは、1957年に亡くなってしまう。

　数値予報のようなコンピュータを用いた技術開発は、純粋科学の研究を目的としていたプリンストンの高等研究所では必ずしも評価が高くなかった。そのためフォン・ノイマンが亡くなると、気象プロジェクトは高等研究所でのコンピュータプロジェクトとともに終了した。

　

しかしながら、それまでに十分に基盤は作られていた。これらのモデルは本の「10-5 数値予報の現業運用化」と「10-7 気候科学の発展」で述べているように、現業の数値予報モデルと気候モデルとして発展していった。現在、毎日の天気予報にはこの数値予報モデルを発展させたものが使われているし、IPCCなどで議論されている地球温暖化の将来予測は、大循環モデルを発展させた気候モデルあるいは地球システムモデルで行われている。

　気象予測モデルは、観測結果の入力から予測の計算結果の導出までにかかる時間が、気象の発現時刻（予測時間）より速くないと意味がない（予測に使えない）という特殊事情がある。フォン・ノイマンは自身でコンピュータを改善して（プログラム内蔵などにして）数値予報が実用化できるほどにコンピュータを高速化しただけでなく、コンピュータ開発のために気象プロジェクトを立ち上げて主導した。

　当時の気象学の分野は小さかったうえに、伝統的な気象学者にとって、全く新しい電子コンピュータを用いた偏微分方程式の数値的解法は、異次元の分野だった。もしフォン・ノイマンがいなければ、数値予報の開発のために人とお金を集めた大規模なプロジェクトを立ち上げることはできなかっただろう。数値予報の開発は、彼が気象予測のための偏微分方程式の数値的解法と、電子コンピュータ技術の両方をよく理解していたからこそできたことだった。もし彼がいなかったら、数値予報の開発は、実際よりはるかに遅れていたに違いない。

（つづく）

 

参照文献

 [1] Shumann G.F. (1989) History of Numerical Weather Prediction at the National Meteorological Center、 Weather and Forecasting、 4 American Meteorological Society、 286-296.

フォン・ノイマンについて（9）数値予報への貢献1

（このブログは 「気象学と気象予報の発達史 」の一部です。） 

 

　フォン・ノイマンは1942年に海底鉱脈の仕事に関わった際に、シカゴ大学の気象・海洋学者であるカール=グスタフ・ロスビー（Carl-Gustaf Rossby, 1898-1957）と知り合いになった[1]。ロスビーは、本の「9-5高層の波と気象予測」で述べているように、上層の長波（プラネタリー波またはロスビー波）の導出を通して大気力学と気象予報を改革した卓越した科学者だった。

フォン・ノイマンは、1945年頃ロスビーから気象予測が主観的な職人芸となっていることを聞き、気象予測のための非線形偏微分方程式（プリミティブ方程式）を電子コンピュータを使って数値計算すれば、職人芸ではなく客観的な予報ができると考えた。

　一方で、膨大な資金を必要とする電子コンピュータの開発には、資金集めのために人々にとってわかりやすい目的が必要だった。彼は実用的な気象予測と気象制御をその目的の一つに据えた。[1]。彼は例えば北極の氷を染めて反射するエネルギー量を減少させれば、アイスランドの気候をハワイのような暖かな気候に変えることができると考えていた[2]。もちろん、現実には気候はさまざまな要素と相互作用をするので、話はそう単純ではない。しかし、そういった気象の複雑性がわかってきたのは、もっと後のことである。

　本の「10-2-3 数値予報への胎動」で述べているように、ものごとをとにかく前に進めることが得意なフォン・ノイマンは、さっそく1946年に海軍などを説得して資金を集めた。そして、電子コンピュータを使った数値予報を研究するために「気象プロジェクト」を立ち上げ、世界の主な気象学者を集めて会議を開いた。それまでばらばらだった予報に対する気象学者たちの考えを、偏微分方程式を数値的に解く数値予報の実現にまとめて、プロジェクトとして一歩前に踏み出させたことは画期的なことだった。

　しかし、本の「9-3 リチャードソンによる数値計算の試み」で述べたように、これはイギリスの気象学者ルイス・リチャードソン（Lewis Richardson, 1881-1953）が第一次世界大戦中に手計算で行って失敗した予報の数値計算を、電子コンピュータに置き換えただけでうまくいくわけではないことははっきりしていた。そのためには本の「10-3-3数値予報の課題解決」で述べているように、解決すべき難問が横たわっていた。

　フォン・ノイマンは、プリンストンの高等研究所でコンピュータと数値予報のための気象学の改善を指揮しつつ、プリンストンからワシントンへ、ニューヨークへ、ロスアラモスへ飛んで、またプリンストンに舞い戻る忙しい日々を送っていた。そのため、気象プロジェクトにそれほど時間を割くことができずに、一時期気象プロジェクトは停滞した。

　その打開のために、1948年に素晴らしい数学的才能を持った若手のアメリカの気象学者ジュール・チャーニー（Jule Charney, 1917-1981）が気象プロジェクトに招かれた。本の「10-3傾圧不安定理論と準地衡風モデル」と「10-4実験的な数値予報の成功」で述べたように、チャーニーによってリチャードソンによる失敗の回避が行われ、電子コンピュータを用いた数値予報のための手法が切り開かれていった。

　数値予報の実験は、当初ENIACではなくその後継マシンで行う予定であったが、後継マシンの開発が遅れたため、本の「10-4-2順圧モデルを使った初めての数値計算」で述べたように、1950年からENIACを使って、順圧モデルという気象の移流のみを予測する簡単化された気象予報モデルで、過去の気象の再現実験が行われた。この際に、順圧モデルを内部記憶装置が小さいENIACで計算できるようにするために、フォン・ノイマンがその手法を開発した。

この結果は、1950年に「順圧渦度⽅程式の数値積分（Numerical integration of the barotropic vorticity equation）」という題で論文に発表された。これは数値予報が実現可能であることを実証した気象学にとって記念碑的な論文となった。この論文の3名の著者の一人としてフォン・ノイマンも入っている。

（つづく）

参照文献

[1]ノーマン・マクレイ、渡辺正、芦田みどり訳（1998）「フォン・ノイマンの生涯」、朝日選書
[2] P. R. Halmos, (1973) The Legend of John Von Neumann, The American Mathematical Monthly, 80, 4, 382-394.

フォン・ノイマンについて（8） 原子爆弾の開発

（このブログは 「気象学と気象予報の発達史 」の一部です。） 

 

　「5 戦争への協力」のところで爆弾の爆発のさせ方によって、爆弾の威力に大きな違いが出ることを述べた。アメリカは原子爆弾を開発するに当たって、その威力を最大限発揮させるにはどうすれば良いかを研究した。特にプルトニウムを用いた原子爆弾は、核分裂させて核爆発を起こすためにプルトニウムを適時に臨界量に持って行く必要があり、爆発させるには爆薬を用いて絶妙なタイミングでプルトニウムを圧縮するために、爆縮という困難な爆発制御を必要とした。

　「5戦争への協力へ」のところで述べたように、フォン・ノイマンは非線形の流体力学と衝撃波の専門家でもあり、指向性爆薬の爆発研究ではアメリカ（おそらく世界でも）で随一だったから、爆縮の開発に彼は最適任者だった。彼は原子爆弾開発プロジェクトであるマンハッタン計画を指揮していたオッペンハイマーに1943年にスカウトされて、開発拠点の一つであるロスアラモス研究所へ行った。当時は使える核物質の量や機密保持の観点から、原子爆弾の爆発実験を重ねるわけにはいかなかったので、彼は爆発の数値実験（シミュレーション）という考え方を用いた。

　フォン・ノイマンは1943年から1945年にかけて数学者のウラム（Stanisław Ulam）とIBM社のパンチカード集計機を用いて、爆縮の設計のため偏微分方程式の数値計算を行った[1]。本の「10-2-1気象計算の機械化」で述べたように、パンチカード集計機は、簡単な加減演算が手計算よりかなり速く正確に行えたため、気候統計などの大量計算にも用いられていた。彼は最終的に火薬と点火装置を32面体に配置して同時に点火し、内部のプルトニウムを圧縮するという「爆縮レンズ」という手法を編み出した。これによって、プルトニウムの圧縮は可能という目途がついた。

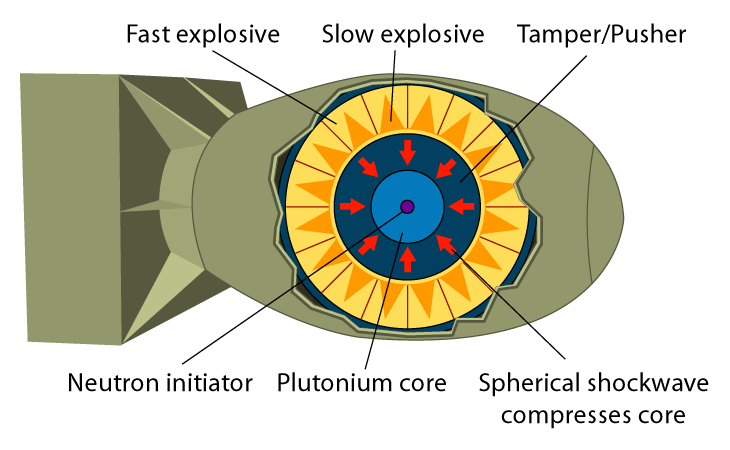爆縮レンズの原理

　フォン・ノイマンはロスアラモスで爆縮の計算だけでなく、原子爆弾開発のいろいろな問題にも関与していた。当時原子爆弾の開発や製造には問題が山積していたが、問題解決に行き詰まった人々は、忙しいフォン・ノイマンが部屋から出たところをつかまえて廊下を歩きながら話を聞いてもらっていた。彼が行き先である会議室に到着するころには、問題の答えか、答えに行き着く道筋が見えていたという[1]。

　なお、広島に落とされたウラン型の原子爆弾は、爆発が確実なため実験は行われなかったが、長崎に落とされたプルトニウム型の原子爆弾は、爆縮の効果を確認するため1945年7月16日にニューメキシコ州アラモゴードで実験的に炸裂させて、核爆発することが確認された。それでも長崎で爆発したプルトニウム型の原子爆弾は、爆発のさせ方によっては威力はもっと大きかったとも言われている。

　フォン・ノイマンと一緒に核の連鎖反応のための中性子拡散の計算を行っていたウラムは、1946年に休憩時にゲームのソリティアをしていた。彼はソリティアを成功させるために、残ったカードの組み合わせの数を推定するより実際に成功する場合を計算機を使って数えた方が速いことに気づき、フォン・ノイマンに相談した。これは多数の確率実験を電子コンピュータを使って行うことによって、統計学的に答えを出すことができるというやり方だった。彼らは中性子拡散の計算にそのやり方を適用することにした。そして、ロスアラモス研究所の物理学者メトロポリス（Nicholas Metropolis）が、1947年にENIACを用いてこのやり方で連鎖反応を初めて計算することに成功した[2]。

　この多数回の試行から解の分布を求めるようなやり方は、カジノで有名な都市名に因んで「モンテカルロ法」と命名された[2]。現在、モンテカルロ法は物理現象の数理解析だけでなく、多重処理方式の電子計算機システム、交通・通信サービス施設のシステム設計や運用のためのシミュレーション、生産ライン、人員配置、在庫管理、建設計画等の生産企業諸部門の設計や運用など広範にわたって使われている。

（つづく）

参照文献

[1]ノーマン・マクレイ、渡辺正、芦田みどり訳（1998）「フォン・ノイマンの生涯」、朝日選書
[2]Gass S. I. (2006) IFORS' Operational Research Hall of Fame: John von Neumann. International Transactions in Operations Research、 13 (1): 85-90

フォン・ノイマンについて（7） 電子コンピュータの開発

（このブログは 「気象学と気象予報の発達史 」の一部です。）  

 

　本の10-2-2「電子計算機の出現」で述べているように、アーサイナス大学の物理学教授ジョン・モークリーは電子工学に強い興味を持っており、1941年頃に太陽黒点周期の気象への影響を調べるために、調和解析機（Harmonic Analyzer）という一種のアナログコンピュータを開発していた。彼はペンシルバニア大学電気工学科のムーア校にいた優れた電気技術者だったプレス・エッカートと知り合いになった。彼らは相互のアイデアを交換して電子式微分解析機を共同で開発することにした。

　この開発は、計算機を砲弾の弾道計算に使いたい陸軍によって、ペンシルバニア大学ムーア校のプロジェクトとして認められることになった。陸軍は支援のために数学者ハーマン・ゴールドシュタインをムーア校へ派遣し、1944年に彼らによって初の汎用の電子式計算機ENIAC（Electronic Numerical Integrator and Computer）が産声を上げた[1]。しかし、ENIACの大きな欠点はプログラム内蔵の機能がないことだった。つまりこの装置において、プログラムの役割は外部配線が担っていたので、新しい計算をするたびに操作者はケーブルをつなぎ換え、スイッチを入れ直し、ダイヤルをいじり、周辺装置を組み替えなければならなかった。

エニアック

https://upload.wikimedia.org/wikipedia/commons/d/d3/Glen_Beck_and_Betty_Snyder_program_the_ENIAC_in_building_328_at_the_Ballistic_Research_Laboratory.jpg

　1944年8月に、フォン・ノイマンはアバディーン駅のホームでゴールドシュタインと偶然に知り合いになった。その際に彼はゴールドシュタインからENIACのことを初めて聞き、その瞬間にENIACに夢中となった。彼は高速での計算が可能になれば、さまざまな分野の非線形偏微分方程式を数値的に解くことができると考えていた。そうなれば、さまざまな分野に全く新しい革新をもたらすことを彼は知り抜いていた。

　フォン・ノイマンは素早く電子コンピュータの本質を理解し、ENIACの演算回路の改良とともに、次に計画されていた計算機EDVACの性能を格段に上げるため新しい構想を練り上げた。彼はENIACを知ってわずか2週間でプログラム内蔵型コンピュータの概念を作り上げ、翌年3月にはコンピュータの改善について有名な「EDVAC報告書の一次稿」を書き上げた。それには現在のコンピュータの基本となっている中央計算部、中央制御部、メモリ部などの構成が整理され、プログラム内蔵の考えが完全に確立されていた[2]。

　ところが、フォン・ノイマンは名誉や金銭的な欲得に薄く、科学の進歩のためには新しい情報を多くの研究者と共有すべきと考えていた。そのため、電子コンピュータの開発を自負して特許を取得しようとしていたエッカートとモークリーとは袂を分かつこととなった。エッカートとモークリーはムーア校を去って会社を興してUNIVACの開発を開始し、ゴールドシュタインは、高等研究所のフォン・ノイマンの元へ行った。

　完成したENIACはペンシルバニア大学からアバディーンにある軍の弾道研究所へ移送され、その際にフォン・ノイマンが内蔵メモリを部分的に追加するなど多少の改修を行ったという。そして1945年末にロスアラモス研究所からの依頼によって、原子爆弾の改善を図るための初めての実用的な計算に使われた。このENIACは、本の10-4-2「順圧モデルを使った初めての数値計算」で述べるように、後にフォン・ノイマンが組織した気象プロジェクトでも使われることとなる。

　フォン・ノイマンは、1945年にプリンストンの高等研究所（IAS）でENIACの後継の独自の新型コンピュータ開発のためのプロジェクトである電子コンピュータプロジェクト（Electronic Computer Project: ECP）を立ち上げた。これは初めて2進法を用いてプログラム内蔵方式で条件付きループが使えるコンピュータを製作するという画期的なものだった。この夢のようなプロジェクトのために、彼は持ち前の説得力でたちまち高等研究所と軍などから30万ドルという莫大な資金を獲得した。これはフォン・ノイマンだからこそできたことだった。この時の電子コンピュータの開発目的には、原子爆弾の改良と気象予測が含まれていた。

　フォン・ノイマンは、1946年から1951年までの電子コンピュータプロジェクトに関する報告書を全て公開した[3]。先ほどの「EDVAC報告書の一次稿」も公開され、この報告書に基づいて、1949年にイギリスのケンブリッジ大学がEDSAC（Electronic Delay Storage Computer）を完成させたのをはじめとして、世界各地でこの報告書に基づいた電子コンピュータが次々に産声を上げることとなった[2]。

　そして1951年に完成した高等研究所の電子コンピュータ（IASマシン）は、既に開発されていた他のどのコンピュータより速かった[3]。後述するように、ENIACで実質24時間かかった順圧モデルを用いた予報のための数値計算は、このIASマシンだと5分以内に終わる計算だった。この高速の計算は、気象学の分野では数値予報と気候モデルという全く新しい分野をもたらした。

　フォン・ノイマンの人望に基づいた説得力によって、電子コンピュータプロジェクトに必要な高額の開発資金を得ることができ、彼の数理学的能力によってこのプロジェクトで新しい論理回路を開発することができた。現在のコンピュータは、この「フォン・ノイマン・アーキテクチャー」と呼ばれている基本構成の延長線上にある。

（つづく）

参照文献

 [1] ENIAC誕生60周年--2人の科学者が作った怪物コンピュータ（https://japan.cnet.com/article/20096729/）CNET Japan

[2]ノーマン・マクレイ、渡辺正、芦田みどり訳（1998）「フォン・ノイマンの生涯」、朝日選書

[3]Electronic Computer Project, Institute for Advanced Study, https://www.ias.edu/electronic-computer-project

フォン・ノイマンについて（6） 経済学への貢献

（このブログは 「気象学と気象予報の発達史 」の一部です。）  

 

　この分野でのフォン・ノイマンの業績は、大きく分けて二つが知られている。一つは1932年にプリンストンの高等研究所での数学セミナーで行った「経済学の方程式いくつかと、プロウェルの不動点定理の一般化について」という講演が端緒となったものである。それは1937年にウィーンでの経済学セミナーの論文集の中で出版され、1980年代になって線形計画法・非線形計画法などの数理経済学を開花させた。

ノイマンがその論文で作ったモデルは「一般経済均衡モデル」と呼ばれ、やがて「フォン・ノイマンの経済成長モデル」という名前がついた。彼が開発した手法から多くのノーベル経済学賞受賞者がでることとなる。フォン・ノイマンはそれまでの経済学を一変させてしまった[1]。

　もう一つは、ドイツ生まれでアメリカで活躍した経済学者オスカー・モルゲンシュテルンと1944年に書いた大著「ゲームの理論」である。これは、彼が1928年に書いた「社会的ゲームの理論について」でのミニマックスの法則が発端となっており、経済学で「意思決定理論」と呼ばれている最も利潤を出すための行動を、ゲーム戦略や組み合わせ理論などを使って定量的に考察するものである。

このゲームの理論は東西冷戦時のアメリカの戦略にも応用された。ゲームの理論での汎用性を持った公理的な考え方は、現在いろんな形で受け継がれてさらに発展し、経営学、政治学、法学、社会学、人類学、心理学、生物学、工学、コンピュータ科学などにも広がっている。

　しかしフォン・ノイマンは、経済学の理論については既存の数学を不十分・不適切につかったところで、その根本にあるあいまいさは追放できないと考えていたようである。数理経済学を深めるには、ニュートンによる微積分の考案に匹敵するような新しい数学の言語が必要であるというのが彼の考えだった[1]。

（つづく）

参照文献

 [1]ノーマン・マクレイ、渡辺正、芦田みどり訳（1998）「フォン・ノイマンの生涯」、朝日選書