(このブログは 「気象学と気象予報の発達史 」の一部です)
4.6 ユール・ウォーカー式
19世紀に各国で始まった気象観測であったが、観測手法や値の単位が異なっていたため、データを交換してもそう簡単には他国では使えなかった。19世紀末頃から気象観測結果の国際的なデータ交換が議論され始め、それは少しずつデータの記録方法の統一へとつながっていった。
そういった背景を受けて、20世紀に入ると世界各地の気象観測の結果を使った相関関係の調査が気象学の研究として行われるようになった。一方でその気象の変動要因として太陽黒点の変動も浮かび上がった。この時間的にある幅でランダムに変動する、つまり揺らぎを持つ準周期的な自然現象が、時系列データを扱う統計学に進歩をもたらした。当時、決定論的な調和解析を用いて太陽黒点の変動が11年周期を持つのではないかということが議論されていた。ところが、イギリスの統計学者ウドニー・ユール(Udny Yule)は、1927年に太陽黒点の変動周期について決定論的にではなく、その強さや周期が揺らぎを持つという前提で新たに2次の自己回帰モデル(AR(2))という手法を考案した。そして、それを用いて太陽黒点の変動周期がおよそ11年であることを示した。これは厳密な調和解析による手法より太陽黒点の周期変動の多くを説明できた [10]。
ウォーカーはユールによる自己回帰モデルの研究の前から、気象の準周期的な現象の問題に取り組んでいた。ユールによる自己回帰モデルの考案の前の1925年に、ウォーカーは南方振動の周期に3~3.25年の幅があることを示して、そういう幅がある周期現象には自己相関を用いた分析が有効であることに気づいていた [14]。しかし、ウォーカーが調査していたダーウィンの気圧変動は、ユールの自己回帰モデルAR(2)より複雑だった。そのため、彼はユールの手法を任意の次数ρの自己回帰モデルAR(ρ)に拡大した。彼は1931年に以下のユール・ウォーカー式を導出した [15]。
定常的なρ次の自己回帰モデルであるAR(ρ) モデルでは、ρ個の時系列現象Xtは、次式で表わされる。

ここで、Φkはk次自己相関パラメータ(t-k時の寄与分)で、atは時刻tに新たに加わった誤差である。ちなみにAR(1)でΦ1を1とおくと、XtはXt-1 から誤差atの幅で動くランダムウォークになる。詳細を省くがこの式において、ρ次のユール・ウォーカー式は次式となる。
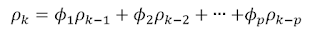
ここで、ρk はk次の自己相関係数である。この式によってk次の自己相関係数はそれより低い次数の自己相関係数の漸化式となっており、自己共分散の式と合わせて自己相関係数の決定を容易にする。また彼は、一般的に自己相関関数が減衰する指数関数と減衰するサイン波の和であることも示している。
この便利なユール・ウォーカー式は、直ちに世の中に根付いたわけではなかった。アメリカの地球物理学者で統計学者のカッツは、自分が見つけたものの中で最も早い利用は1949年だったと述べている [10]。しかし、この式は近代的な時系列解析における画期的な発見であり、現在では自己相関を扱う数多くの分野で広く使われている。しかし、細分化されて専門分野化された現在の科学において、前述のカッツは気象学での南方振動と統計学のユール・ウォーカー式が、どちらも同一人物による同一の研究から生まれたものであることを、どれだけの人々が認識しているだろうかと疑問を投げかけている。
(つづく)
参考文献(このシリーズ共通)
[1] Taylor I.G., 1962: Gilbert Thomas Walker. 1868-1958. Biographical Memoirs of Fellows of the Royal Society, The Royal Society, 8, 166-174.
[2] Walker M.J., 1997: Pen Portrait of Sir Gilbert Walker, CSI, MA, SCD, FRS. Weather, Royal Meteorological Society, 52, 217-220.
[3] Walker T.G., 1901: boomerangs. Nature, Nature Publishing Group, 64, 338-340.
[4] 田家康, 2011: 世界史を変えた異常気象, 日本経済新聞社.
[5] Normand C., 1953: Monsoon seasonal forecasting. Quarterly Journal of the Royal Meteorological Society, Royal Meteorological Society, 79, 463-473.
[6] Pisharoty R.P., 1990: Sir Gilbert Walker-pioneer meteorologist and versatile scientist. CURRENT SCIENCE, Current Science Association, 59, 121-122.
[7] Walker T.G., 1923: Correlation in seasonal variations of weather. VIII. A preliminary study of world-weather. Memoirs of the Indian Meteorological Department, Indian Meteorological Department, 24, 75-131.
[8] Hildebrandsson H.H., 1897: Quelques recherches sur les entres d'action de l'atmosphere. Kongl. Svenska vetenskaps-akademiens handlingar, P.A. Norstedt & s?ner, 29, 33pp.
[9] Lockyer J. N. and Lockyer W. J. S., 1903: On the similarity of the short-period pressure variation over large areas. Royal Society of London, Proceedings of The Royal Society, 71, p467-476.
[10] Katz W. R., 2002: Sir Gilbert Walker and a Connection between El Nino and Statistics, Institute of Mathematical Statistics, Statistical Science, 17, p97-112.
[11] Walker T. G., 1924: Correlation in seasonal variations of weather. IX. A further study of world weather. Indian Meteorological Department, Memoirs of the Indian Meteorological Department, 24, p275-332.
[12] Walker T. G., 1933: Seasonal Weather and its Prediction, Nature Publishing Group, Nature, November 25, p805-808.
[13] Walker T. G., 1918: Correlation in seasonal variations of weather, Royal Meteorological Society, Quarterly Journal of the Royal Meteorological Society, 44, p223-224.
[14] Walker T. G., 1925: On periodicity, Royal Meteorological Society, Quarterly Journal of the Royal Meteorological Society, 51, p337-346.
[15] Walker T. G., 1931: On periodicity in series of related terms, Royal Society of London, Proceedings of The Royal Society of London, Ser. A 131, p518-532.